I’ve been picking up and working through some of the exercises in Bayesian Reasoning and Machine Learning — a book I’ve been finding extremely readable and enjoyable to work through.

The official solutions are restricted to instructors, which makes it a little hard to confirm if I’m going down on the right path or not; there are some hits on google when searching for solutions — but I’m a little skeptical of the correctness of some of them. I’ll try and capture some of my solutions in this post for the next person working through the book by themselves.

(The book is available online here.)

Exercise 1.5

This was a tricky one: there’s a description of a solution from the original source of the problem at http://understandinguncertainty.org/dishonesty, except that this variation has an additional twist — it’s not any person who triggers the scanner, but the first person to trigger the scanner. You can see a Twitter thread where we flail around wondering about a solution here and my final solution here.

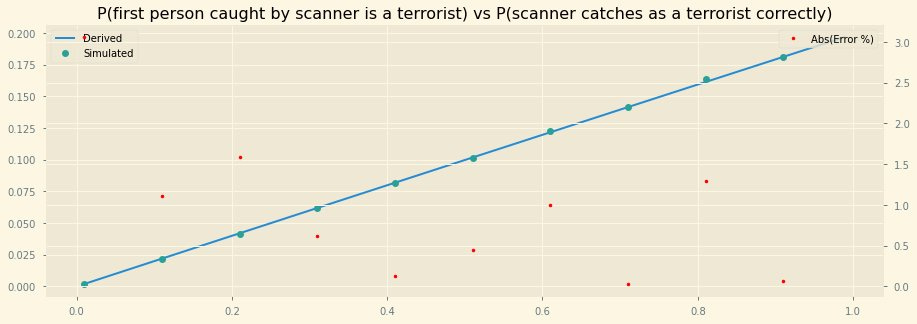
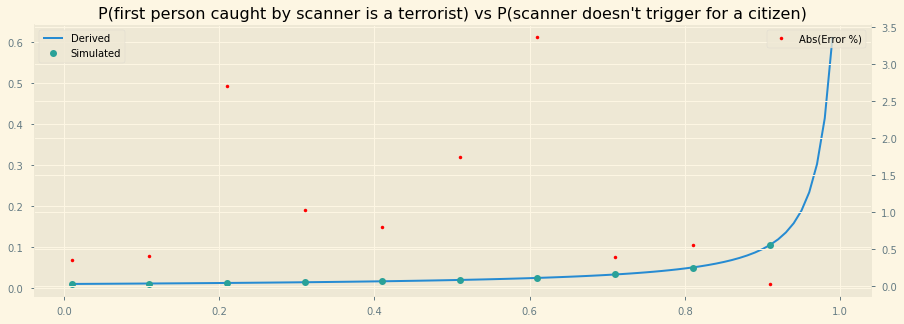
A notebook plotting out the derived solution is here. The derivation is basically based on Baye’s theorem — to have a general solution, defining

• a = probability that a terrorist will set off the scanner (.95 in the problem)

• b = probability that a citizen doesn’t set off the scanner (.95 again)

• k = number of passengers in the plane

Then, expressing the problem in terms of the person who set off the scanner — which can be evaluated as a marginal solution over all possible positions of x from 1 to k.

P(x is a Terrorist | x is the first person to set off the scanner) = P(x is the first person to set off the scanner | x is a terrorist) * P(x is a terrorist) / P(x is the first person to set off the scanner)

Here,

• P(x is a terrorist) over all possible passengers in the flight = Sum from 1 -> k where the probability of there being a terrorist is 1/k; which turns out to be 1. (Our prior is that exactly 1 of the k passengers is a terrorist)

• P(x is a terrorist | x is the first person to set off the scanner)

  • = Sum i from 1 -> k over P(No one from 1 -> i - 1 triggered the scanner | x at point i is the terrorist) * P(x triggers the scanner | x at point i is the terrorist)

  • = Sum (a * b^(i - 1))

  • = a * (1 - b^(k - 1)) / (1 - b) (using the sum of a geometric series)

• P (x is the first person to set off the scanner) over all possible positions of x

  • = P (anyone sets off the scanner)

  • = 1 - P (no-one sets off the scanner)

  • = 1 - (1 - a) * b ^ (k - 1)

Putting it all together, the answer I get is

P(x is a terrorist | x is the first person to set off the scanner)

• = a * (1 - b ^(k - 1)) / (1 - b) / (1 - (1 - a) * b ^ (k - 1))

• = 0.1889 plugging in a = .95, b = .95, k = 100

I enjoyed exploring this problem a lot; some of my primary takeaways include:

• Nothing quite beats a simulation to get answers that I can trust; my intuition is pretty faulty in general.

• Even with 95% odds of catching the right person, the scanner will only catch them <20% of the time. Improving the odds of catching the right person don’t help improve this much.

  

• Increasing the number of people in the aeroplane dramatically reduces the odds of successfully catching a terrorist.

  

• Reducing the chances that the scanner goes off for a normal person gives the most return for investment just because k >> 1. The derived solution is roughly proportional to 1 / probability of triggering the scanner for a normal person.

  

• This doubles down on the fact that even very high quality detection for very rare events means most likely instances of a detection are likely to be false-positives. Reducing the odds of a false-positive seems to have the greatest possible impact.